3. Another Example: colliding winds (2D)

3.1. Introduction

This example is taken from Stevens et al. (1992), section 4.1, modelling the colliding winds of the binary system V444 Cyg. This eclipsing binary system contains a Wolf-Rayet (WR) star (of spectral type WN5) with a an O6 companion. We assume that the WR star is the primary because it is more evolved than the O6 star.

The properties of the stars (taken from Stevens et al.) are as follows for the primary (WR):

  • mass-loss rate \(\dot{M} = 1.4\times10^{-5} \,\mathrm{M}_\odot \, \mathrm{yr}^{-1}\)

  • wind speed \(v_\infty = 2000 \,\mathrm{km\,s}^{-1}\)

  • radius \(R_\star = 2.9 \,\mathrm{R}_\odot\)

  • temperature \(T_\mathrm{eff}=35\) kK

and for the secondary (O6):

  • mass-loss rate \(\dot{M} = 10^{-6} \,\mathrm{M}_\odot \, \mathrm{yr}^{-1}\)

  • wind speed \(v_\infty = 2000 \,\mathrm{km\,s}^{-1}\)

  • radius \(R_\star = 10 \,\mathrm{R}_\odot\)

  • temperature \(T_\mathrm{eff}=40\) kK

The system has an orbital period of 4.2 days, although in this 2D simulation we ignore the orbital motion and treat the wind-wind interaction as though the stars were at rest in an inertial frame with cylindrical symmetry along the line connecting the stars. The separation of the stars is taken as \(2.8\times10^{12}\) cm.

The shocked wind in the wind-collision region should be quite strongly radiative, and this has a big effect on the hydrodynamics of the wind-collision region. In this example the simulation domain has dimensions \(z\in[-1.024,1.024]\times10^{13}\) cm, \(R\in[0,1.024]\times10^{13}\) cm, resolved by \(640\times320\) grid cells, and 2 refined levels centred on the origin (i.e. 3 levels in total). The finest grid contains the two stars.

3.2. Running the simulation

  • Follow the preparation steps in Running an example simulation.

  • Download the parameter file param_V444Cyg_d2l3n320.txt to a local directory.

  • Set up the initial conditions:

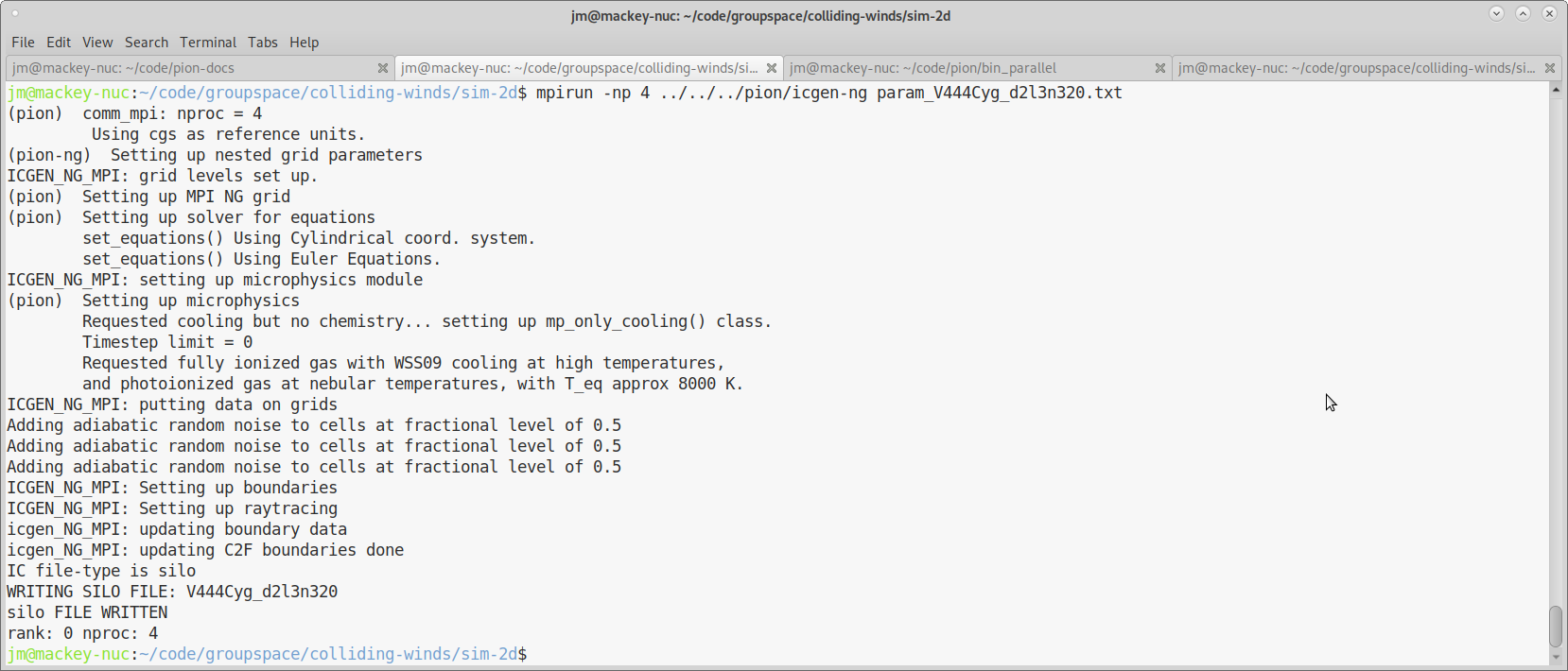
    Stdout for setting up initial conditions

    Fig. 3.1 Screenshot of setting up initial conditions.

  • We first run the simulation with adiabatic hydrodynamics (i.e. radiative cooling switched off) by selecting cooling=0 as a command-line option. The simulation runs faster to set up the wind-wind collision:

    Stdout for starting simulation with adiabatic hydrodynamics

    Fig. 3.2 Screenshot of starting PION for the colliding-winds simulation.

  • After about 60,000 seconds a stable wind-wind collision has been set up, shaped like a bow shock because the O star has a much weaker wind than the WR star. We stop the simulation after 13824 steps and look at the results using VisIt:

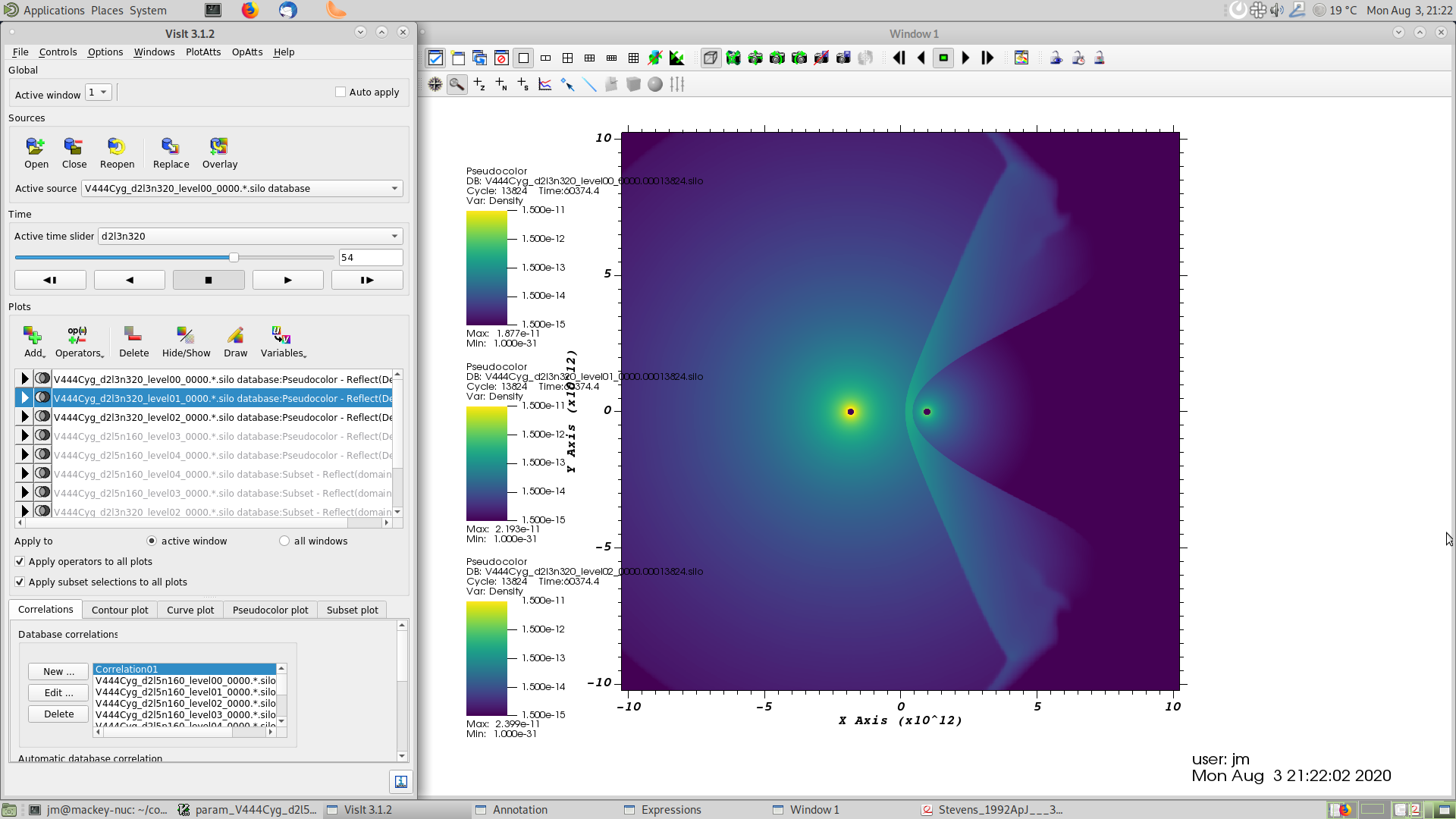
    V444 Cyg colliding wind binary with adiabatic hydrodynamics

    Fig. 3.3 Screenshot of the wind-wind collision for V444 Cyg with adiabatic-hydrodynamics.

  • We then restart with radiative cooling: cooling=8 means that we use an optically thin cooling function appropriate for photoionized gas. This is probably not appropriate for the very high densities found in the wind-collision region, but the important point is that the cooling time is shorter than the advection time for the shocked wind, and so the gas cools and is compressed to very high densities.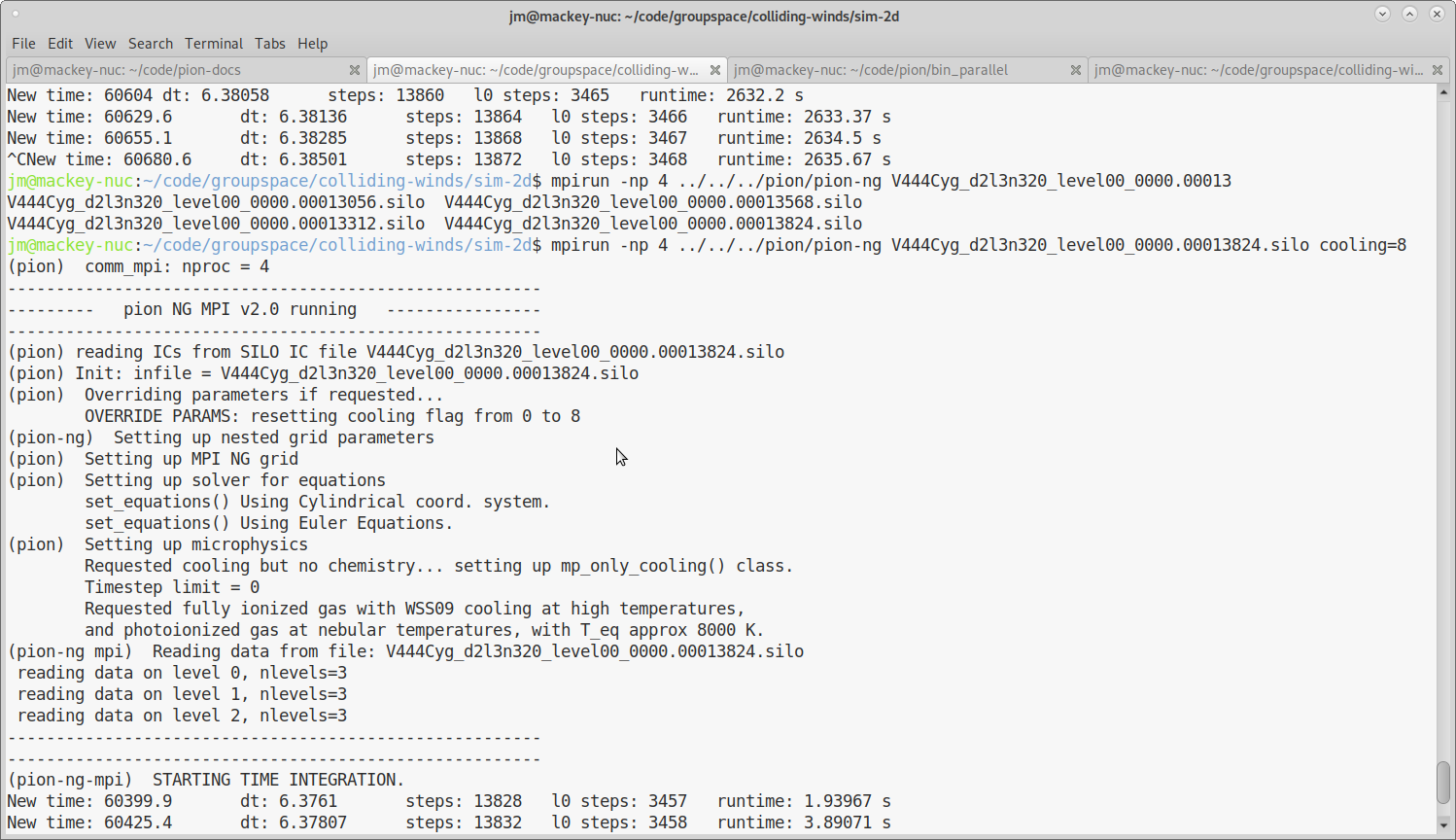

    Stdout for restarting simulation with radiative cooling

    Fig. 3.4 Screenshot of restarting PION for the colliding-winds simulation, with radiative cooling switched on.

  • The wind-collision region gets narrower as the shocked gas cools rapidy, and eventually is subject to thin-shell instability. After some time the constraints imposed by the symmetry axis in 2D lead to unphysical extreme oscillation of the shock front between the two stars, but before this happens the dynamics of the wind are dramatically different from the adiabatic case.

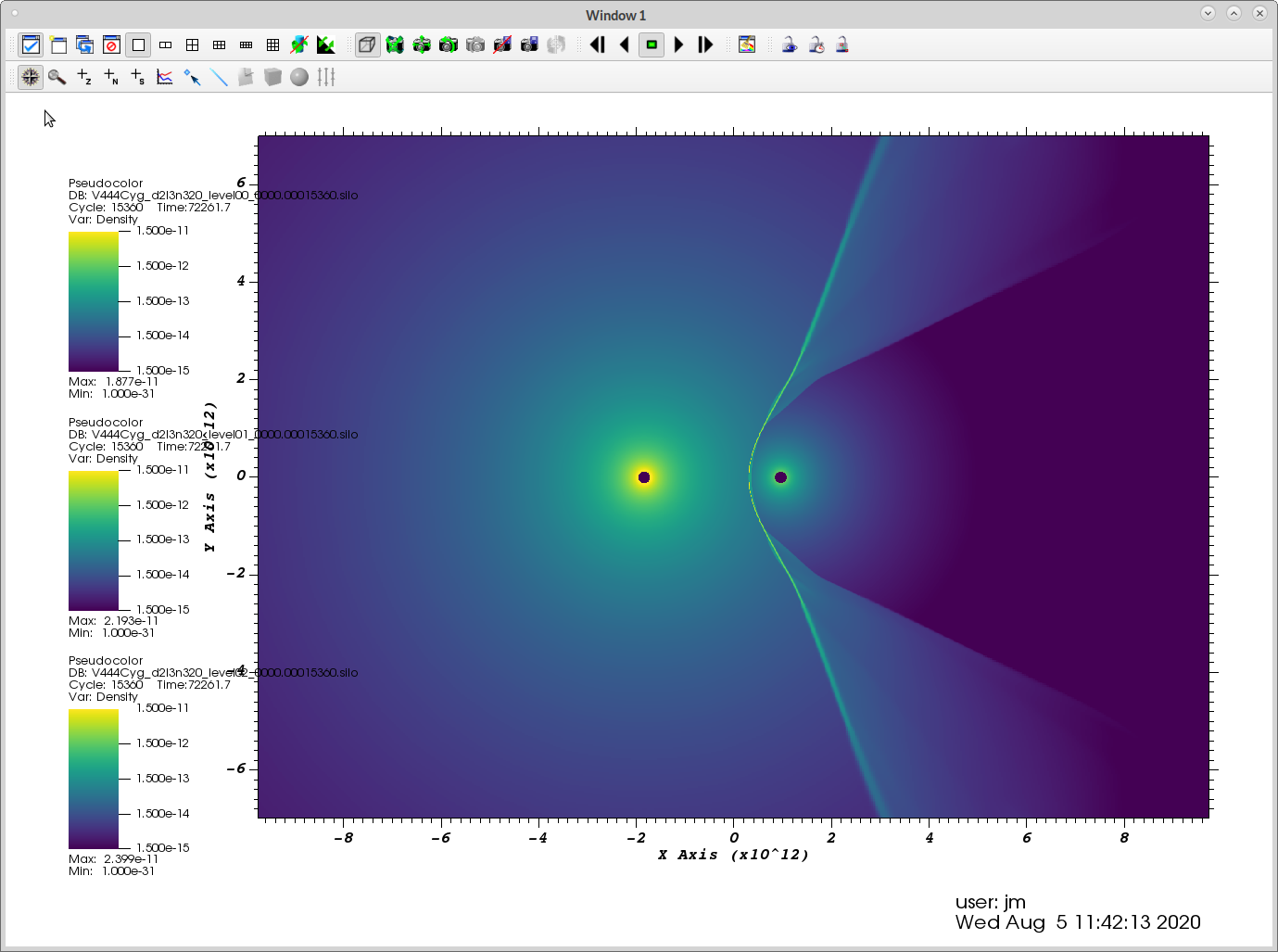
    V444 Cyg colliding wind binary with radiative cooling

    Fig. 3.5 Screenshot of the wind-wind collision for V444 Cyg just after cooling has been switched on.

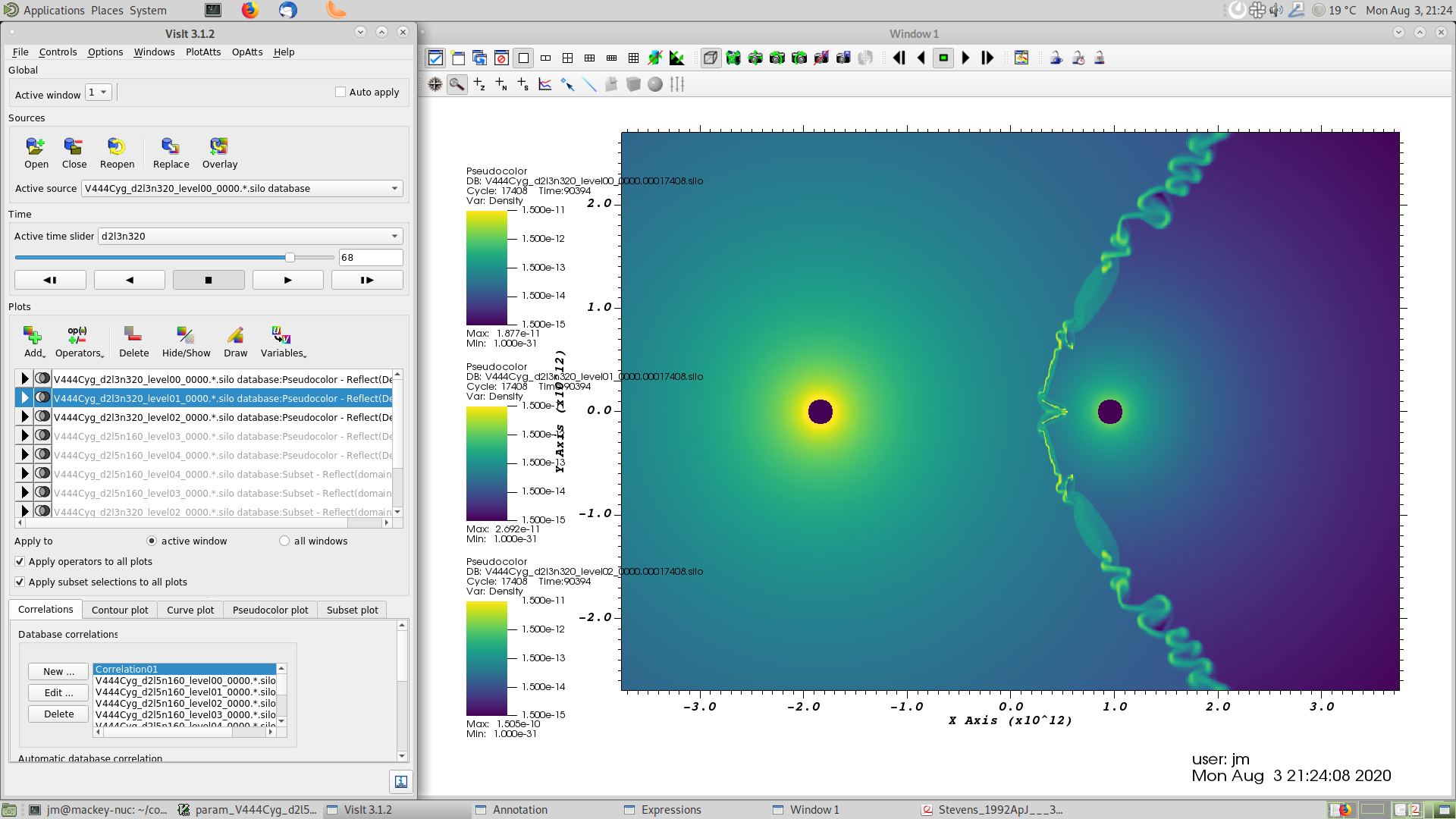
    V444 Cyg colliding wind binary with radiative cooling

    Fig. 3.6 Screenshot of the wind-wind collision for V444 Cyg zoomed in to the highest level of refinement.

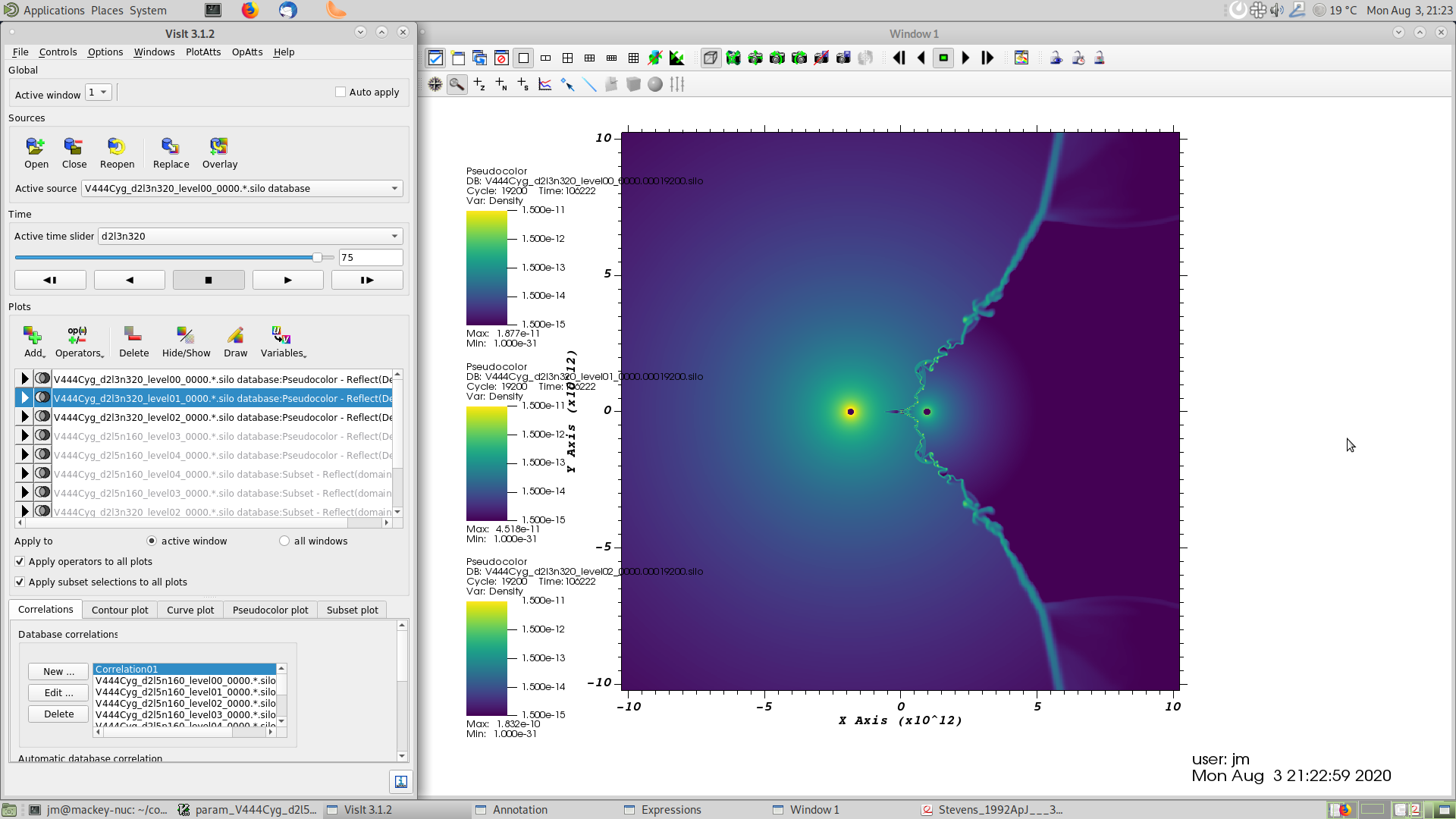
    V444 Cyg colliding wind binary with radiative cooling

    Fig. 3.7 Screenshot of the wind-wind collision for V444 Cyg at the final snapshot.

An animation of the simulation can be viewed here. This simulation took about 3 hours to run using 4 MPI processes on an Intel NUC. The equivalent 3D simulation would take about 10 thousand core-hours.